19. Perturbation modeling

19.1. Motivation

Advances in single-cell experimental protocols allow for massively multiplexed experiments to measure hundreds of thousands of cells under thousands of unique conditions. These are commonly termed “perturbations”, which are temporary or permanent changes caused by an external influence [Srivatsan et al., 2020]. Recently, such technologies have been adapted to profile CRISPR-Cas9 with multimodal readouts [Frangieh et al., 2021, Papalexi et al., 2021], genome-wide perturbations [Replogle et al., 2021], and combinatorial perturbations [Wessels et al., 2022]. Despite experimental advances, exploring the massive perturbation space of combinatorial gene knock-outs or drug combinations remains challenging. The vast exploration space motivated the development of computational approaches for modeling single-cell perturbation responses [Ji et al., 2021].

Perturbation modeling entails areas[Ji et al., 2021]:

1. Perturbation responses: Predicting omics signatures after a perturbation given information about the control and treatment conditions. Predictions can be evaluated by the correlation of predicted features with respect to the true values. It is further possible to predict phenotypic measurements such as IC50 values, area under the dose response curve, toxicity and viability.

2. Targets and mechanisms: Predicting targets and mechanisms of perturbation using omics measurements. Drug mode of actions can be identified with perturbation modeling even for uncharacterized compounds.

3. Perturbation interactions: Predicting combinatorial effects of perturbations to gain an understanding of interlinked effects between genetics and drugs or combinations of drugs.

4. Chemical properties: Predicting chemical properties of perturbations using omics measurements such as molecular fingerprints, R groups, pharmacophores or even complete compounds.

Robust and accessible tooling for all of these steps is still under development. Hence, we will solely introduce three approaches for a subset of these tasks that can be tackled with single-cell perturbation data in the following sections:

1. Finding the cell types that were most affected by perturbations using Augur applied to Kang 2018 [Kang et al., 2018].

2. Predicting the transcriptional response of single cells to perturbations using scGen applied to Kang 2018 [Kang et al., 2018].

3. Quantifying the sensitivity of genetic CRISPR perturbations using Mixscape applied to Papalexi 2021 [Papalexi et al., 2021].

19.2. Identifying the cell types most affected by perturbations

19.2.1. Motivation

Perturbations rarely have the same effect on all cells. In particular, different cell types or cells in different states in their cell cycle can be affected to varying degrees. Here we will leverage Augur by Skinnider et al. [Skinnider et al., 2021, Squair et al., 2021], which provides one way of quantifying the degree of response, for this purpose.

Augur model

Augur aims to rank or prioritize cell types according to their response to experimental perturbations given single-cell gene expression data. The basic idea is that in the space of molecular measurements, cells reacting heavily to induced perturbations are more easily separated into perturbed and unperturbed groups than cell types with little or no response. This separability is quantified by measuring how well experimental labels (for example, treatment and control) can be predicted within each cell type. Augur trains a machine learning model predicting experimental labels for each cell type in multiple cross-validation runs and then prioritizes cell type response according to metric scores measuring the accuracy of the model. For categorical data the area under the curve is the default metric and for numerical data the concordance correlation coefficient is used as a proxy for model accuracy, which in turn approximates perturbation response.

19.2.2. Limitations of Augur

Since Augur determines the degree of perturbation responses, it requires distinct cell types. If cell type labeling is challenging due to ongoing continuous, smooth processes or trajectories of gene expression such as cell differentiation, Augur might not allow for fine-grained enough rankings. Constructing a clustering tree describing the relationships of different clusters, which were used for cell type annotation, and applying Augur to all possible clustering resolutions, could determine the most suitable resolution and therefore annotation for the perturbation of interest [Squair et al., 2021].

Further, cell types mediating tissue- or organism-level responses to specific perturbations might themselves comprise subpopulations of responder and non-responder cells. The assignment of cells into responder and non-responder cells itself can be inaccurate because cells of a given cell type could fall along a continuous trajectory of perturbation response intensity. However, Augur does not decipher the individual cells’ perturbation responses and simply aggregates them as averages for the cell types [Squair et al., 2021].

Some perturbation effects might originate primarily from a change in relative abundance of a particular cell type. The subsampling procedure in Augur, however, discards any information about the relative abundances. In fact, Augur samples equal numbers of cells from each condition prior to cross-validation. Any change in the abundance of a particular cell type could be accompanied by changes in the intrinsic transcriptional profile of that cell type. Strong perturbations could even lead to scenarios where specific cell types are depleted completely or suddenly arise only when perturbed. Hence, it is advisable to perform differential abundance tests for every cell type to help contextualize the Augur analysis results [Squair et al., 2021].

Here, we will use a fast reimplementation of the original R implementation of Augur using the perturbation analysis toolbox pertpy. pertpy leverages the scverse ecosystem and is therefore fully compatible with AnnData in the Python ecosystem.

19.2.3. Predicting cell type prioritization for IFN-β stimulation

To demonstrate Augur, we will use the Kang dataset, which is a 10x droplet-based scRNA-seq peripheral blood mononuclear cell (PBMC) dataset from 8 Lupus patients before and after 6h-treatment with INF-β (16 samples in total)[Kang et al., 2018].

Our goal here is to decipher which cell types were most affected by INF-β treatment.

First, we import pertpy and scanpy.

import warnings

warnings.filterwarnings("ignore")
warnings.simplefilter("ignore")

# This is required to catch warnings when the multiprocessing module is used
import os

os.environ["PYTHONWARNINGS"] = "ignore"

import pertpy as pt
import scanpy as sc

pertpy provides a convenient data loader to access the Kang dataset.

adata = pt.dt.kang_2018()

We rename label to condition and the conditions themselves for improved readability.

adata.obs.rename({"label": "condition"}, axis=1, inplace=True)
adata.obs["condition"].replace({"ctrl": "control", "stim": "stimulated"}, inplace=True)

This dataset contains PBMCs [Kang et al., 2018] across seven different cell-types.

adata.obs.cell_type.value_counts()

cell_type
CD4 T cells          11238
CD14+ Monocytes       5697
B cells               2651
NK cells              1716
CD8 T cells           1621
FCGR3A+ Monocytes     1089
Dendritic cells        529
Megakaryocytes         132
Name: count, dtype: int64

We now create an Augur object using pertpy based on our estimator of interest to measure how predictable the perturbation labels for each cell type in the dataset are. The options for the estimator are random_forest_classifier or logistic_regression_classifier for categorical data and random_forest_regressor for numerical data. All estimators make use of a Params class to define further parameters. Here, we will use a random_forest_classifier which is generally a solid and fast choice and suits our categorical data.

ag_rfc = pt.tl.Augur("random_forest_classifier")

Next, we need to load the AnnData object into a format that Augur is comfortable with. This can be easily done with the load function of our Augur object.

loaded_data = ag_rfc.load(adata, label_col="condition", cell_type_col="cell_type")
loaded_data

AnnData object with n_obs × n_vars = 24673 × 15706
    obs: 'nCount_RNA', 'nFeature_RNA', 'tsne1', 'tsne2', 'label', 'cluster', 'cell_type', 'replicate', 'nCount_SCT', 'nFeature_SCT', 'integrated_snn_res.0.4', 'seurat_clusters', 'y_'
    var: 'name'
    obsm: 'X_pca', 'X_umap'

This allows us to run Augur with the predict function. Generally, Augur can be run in two modes:

1. A feature selection based on the original Augur implementation (select_variance_feature=True) that is also the default. This approach removes features with little cell-to-cell variation within that cell type. We refer to the Augur Nature Protocols paper for more details[Squair et al., 2021]. When this feature selection is chosen the results are very similar to the Augur implementation in R.

2. A feature selection based on scanpy.pp.highly_variable_genes. This feature selection reduces the number of genes that are taken into account for model training and might result in inflated Augur scores, because the highly variable genes are very useful to separate cell types. However, this mode is faster and recovers effects of perturbations on cell types very well. We recommend it for very large datasets with perturbations that are expected to have a strong effect on specific cell types.

Since we do not expect INF-β to have an exceptional effect on specific cell types, we run Augur with the original Augur feature selection. To further increase the resolution, we set the subsample_size to 20 (default: 50) which corresponds to the number of cells to randomly draw per cell type.

v_adata, v_results = ag_rfc.predict(
    loaded_data, subsample_size=20, n_threads=4, select_variance_features=True, span=1
)

v_results["summary_metrics"]

Set smaller span value in the case of a `segmentation fault` error.

Set larger span in case of svddc or other near singularities error.

	CD14+ Monocytes	CD4 T cells	Dendritic cells	NK cells	CD8 T cells	B cells	FCGR3A+ Monocytes	Megakaryocytes
mean_augur_score	0.920476	0.669376	0.847007	0.673299	0.626247	0.783628	0.888934	0.512619
mean_auc	0.920476	0.669376	0.847007	0.673299	0.626247	0.783628	0.888934	0.512619
mean_accuracy	0.817033	0.601172	0.744249	0.610330	0.575714	0.674505	0.780330	0.510513
mean_precision	0.835072	0.630593	0.779699	0.642700	0.587059	0.742801	0.792996	0.526175
mean_f1	0.806636	0.564695	0.735157	0.591230	0.552114	0.633906	0.780933	0.406510
mean_recall	0.826349	0.575714	0.756032	0.616984	0.580000	0.622540	0.816508	0.388413

The result table contains several evaluation metrics for the fitted model. For the interpretation of the cell type prioritization of the IFN-β response, only the mean_augur_score is relevant, which corresponds to the mean_auc. The higher the value, the easier it is for the fitted model to discern between control and perturbed cell states. Hence, the perturbation effect was stronger for this cell type. Let’s visualize this effect.

lollipop = ag_rfc.plot_lollipop(v_results)

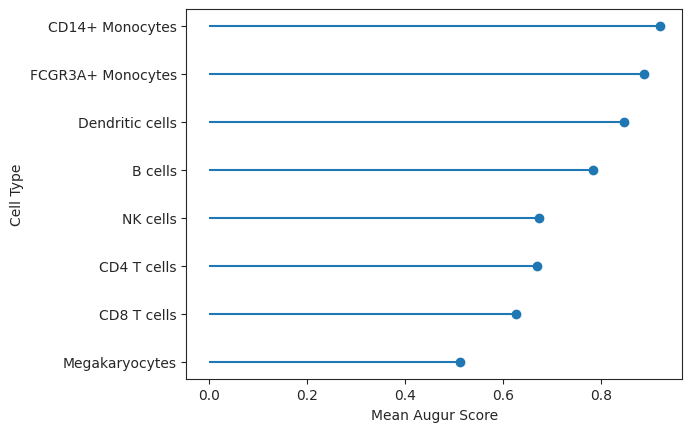
As observed, CD14+ Monocytes were the most affected by IFN-β whereas Megakaryocytes were the least affected. This corresponds roughly to the number of differentially expressed genes in the original publication for the respective cell types [Kang et al., 2018].

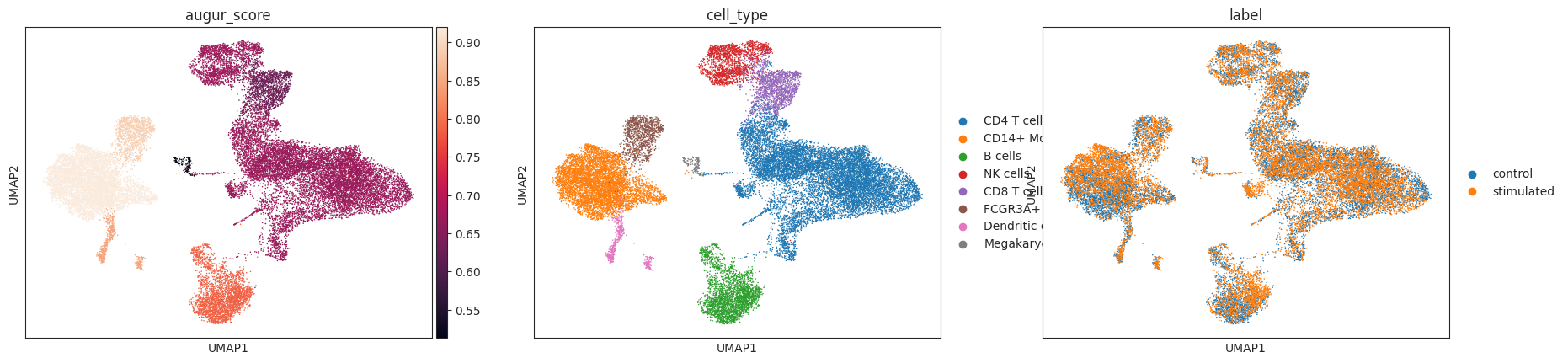
The corresponding mean_augur_score is also saved in v_adata.obs and can be plotted in a UMAP.

sc.pp.neighbors(v_adata)
sc.tl.umap(v_adata)

sc.pl.umap(adata=v_adata, color=["augur_score", "cell_type", "label"])

19.2.4. Determining the most important genes for the prioritization

The genes that contribute the most to the prioritization, as reflected by the augur score, correspond to the feature importances of our model. These feature importances are saved in the results object and can be easily plotted.

important_features = ag_rfc.plot_important_features(v_results)

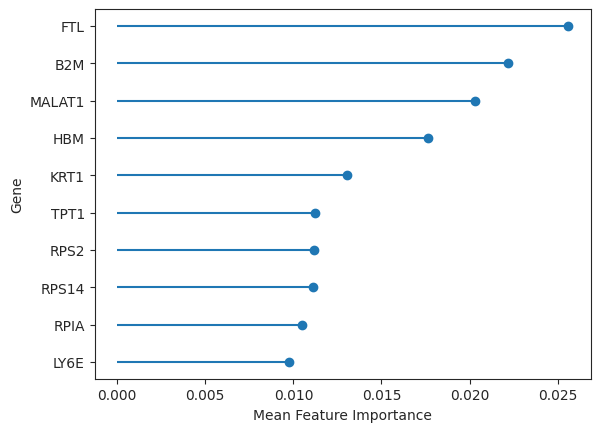
These genes could now be further explored concerning, for example, their role in pathways or other gene sets. However, since Augur performs inference on the cell type level, it does not directly determine the individual genes that are involved in the perturbation response. The authors of Augur themselves suggest using differential gene expression tests to be both conceptually and pragmatically a more appropriate approach to the inference at the level of individual genes [Squair et al., 2021].

19.2.5. Differential prioritization

Augur is also able to perform differential prioritization by executing a permutation test to identify cell types with statistically significant differences in area under the curve (AUC) between two different rounds of cell type prioritization (for example a response to drugs A and B compared to untreated control).

Bhattacherjee et al. offered mice cocaine, and took samples of the prefrontal cortex for scRNA-seq at 48 hours and 15 days post withdrawal[Bhattacherjee et al., 2019].

We will now evaluate the effect of the withdraw_15d_Cocaine and withdraw_48h_Cocaine conditions compared to Maintenance_Cocaine. Basically, differential prioritization is obtained through a permutation test of the difference in AUC between two sets of cell-type prioritizations, compared with the expected AUC difference between the same two prioritizations after random permutation of sample labels[Squair et al., 2021]. In this procedure, the user first performs cell-type prioritization on drug A (withdraw_15d_Cocaine) and drug B (withdraw_48h_Cocaine) separately, then calculates the AUC difference between drug A and drug B. To compute the statistical significance of the AUC difference , an empirical null distribution of AUC differences is then calculated for each cell type by permuting the sample labels, then repeating cell-type prioritization in the permuted data. Permutation P-values are then calculated. This procedure thus enables the identification of statistically significant differences in cell-type prioritization between conditions, as well as the condition in which the cell type is more transcriptionally separable.

Each variation is run once in default mode and once in permute mode to allow us to perform the permutation test. As a first step, we fetch the bhattacherjee dataset using pertpy and create an Augur object that again uses a random forest classifier.

bhattacherjee_adata = pt.dt.bhattacherjee()
ag_rfc = pt.tl.Augur("random_forest_classifier")

Next, we run Augur on Maintenance_Cocaine and withdraw_15d_Cocaine using both augur_mode=default and augur_mode=permute as previously described. Note that we log normalize the dataset for a simple normalization.

sc.pp.log1p(bhattacherjee_adata)

# Default mode
bhattacherjee_15 = ag_rfc.load(
    bhattacherjee_adata,
    condition_label="Maintenance_Cocaine",
    treatment_label="withdraw_15d_Cocaine",
)

bhattacherjee_adata_15, bhattacherjee_results_15 = ag_rfc.predict(
    bhattacherjee_15, random_state=None, n_threads=4
)
bhattacherjee_results_15["summary_metrics"].loc["mean_augur_score"].sort_values(
    ascending=False
)

Filtering samples with Maintenance_Cocaine and withdraw_15d_Cocaine labels.

Set smaller span value in the case of a `segmentation fault` error.

Set larger span in case of svddc or other near singularities error.

Oligo         0.801417
Astro         0.769116
Microglia     0.743707
OPC           0.743605
Inhibitory    0.656202
NF Oligo      0.625692
Excitatory    0.623923
Endo          0.588481
Name: mean_augur_score, dtype: float64

# Permute mode
bhattacherjee_adata_15_permute, bhattacherjee_results_15_permute = ag_rfc.predict(
    bhattacherjee_15,
    augur_mode="permute",
    n_subsamples=100,
    random_state=None,
    n_threads=4,
)

Set smaller span value in the case of a `segmentation fault` error.

Set larger span in case of svddc or other near singularities error.

Now let’s do the same for Maintenance_Cocaine and withdraw_48h_Cocaine.

# Default mode
bhattacherjee_48 = ag_rfc.load(
    bhattacherjee_adata,
    condition_label="Maintenance_Cocaine",
    treatment_label="withdraw_48h_Cocaine",
)

bhattacherjee_adata_48, bhattacherjee_results_48 = ag_rfc.predict(
    bhattacherjee_48, random_state=None, n_threads=4
)

bhattacherjee_results_48["summary_metrics"].loc["mean_augur_score"].sort_values(
    ascending=False
)

Filtering samples with Maintenance_Cocaine and withdraw_48h_Cocaine labels.

Set smaller span value in the case of a `segmentation fault` error.

Set larger span in case of svddc or other near singularities error.

Astro         0.624898
OPC           0.598050
NF Oligo      0.592619
Microglia     0.587789
Inhibitory    0.560000
Oligo         0.557630
Endo          0.540272
Excitatory    0.527143
Name: mean_augur_score, dtype: float64

# Permute mode
bhattacherjee_adata_48_permute, bhattacherjee_results_48_permute = ag_rfc.predict(
    bhattacherjee_48,
    augur_mode="permute",
    n_subsamples=100,
    random_state=None,
    n_threads=4,
)

Set smaller span value in the case of a `segmentation fault` error.

Set larger span in case of svddc or other near singularities error.

Skipping NF Oligo cell type - 79 samples is less than min_cells 100.

This allows us to take a look at the augur scores of the two runs in a scatterplot. The diagonal line is the identity function. If the values were the same they would be on the line.

scatter = ag_rfc.plot_scatterplot(bhattacherjee_results_15, bhattacherjee_results_48)

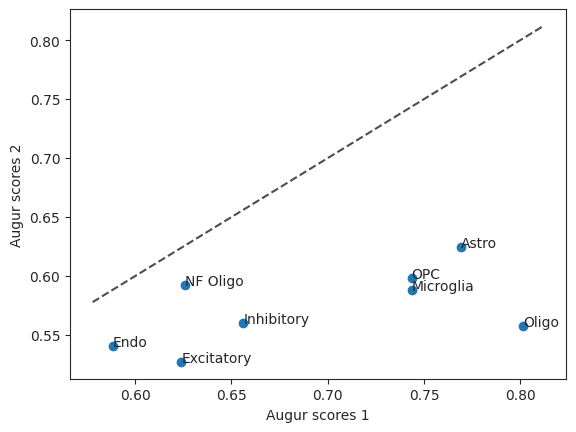
To figure out which cell type was most affected when comparing withdraw_48h_Cocaine and withdraw_15d_Cocaine we can run differential prioritization.

pvals = ag_rfc.predict_differential_prioritization(
    augur_results1=bhattacherjee_results_15,
    augur_results2=bhattacherjee_results_48,
    permuted_results1=bhattacherjee_results_15_permute,
    permuted_results2=bhattacherjee_results_48_permute,
)
pvals

	cell_type	mean_augur_score1	mean_augur_score2	delta_augur	b	m	z	pval	padj
0	Astro	0.769116	0.624898	-0.144218	1000	1000	-10.058451	0.001998	0.002331
1	Microglia	0.743707	0.587789	-0.155918	974	1000	-9.252930	0.053946	0.053946
2	Endo	0.588481	0.540272	-0.048209	1000	1000	-3.010936	0.001998	0.002331
3	Oligo	0.801417	0.557630	-0.243787	1000	1000	-15.904970	0.001998	0.002331
4	Inhibitory	0.656202	0.560000	-0.096202	1000	1000	-6.018999	0.001998	0.002331
5	OPC	0.743605	0.598050	-0.145556	1000	1000	-8.786800	0.001998	0.002331
6	Excitatory	0.623923	0.527143	-0.096780	1000	1000	-7.399583	0.001998	0.002331

The p-value, following the R Augur implementation is calculated using b, the number of times permuted values are larger than original values and m, the number of permutations run. Since b is the same for all cells but Microglia, the p-value is the same for these as well.

diff = ag_rfc.plot_dp_scatter(pvals)

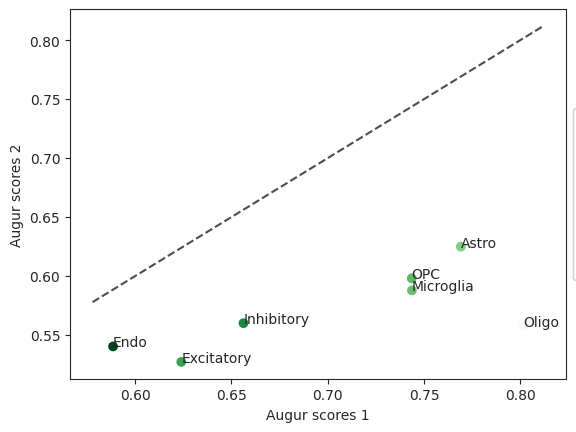
In this case the cell type “Inhibitory” is not very different between the two compared cell types which may indicate that permanent damage was inflicted.

19.3. Predicting IFN-β response for CD4-T cells

Many perturbation response modeling methods aim to forecast transcriptomic responses to stimuli, be it drugs, genetic knock-outs, or disease, for unseen populations where the perturbation response has not been measured, to help facilitate experimental design and hypothesis generation. The failure to capture cells treated with a perturbation could happen when a specific population could not be measured due to experimental or sample failure (e.g., failed cell sorting), high experimental costs prohibiting exploring all possibilities, and rare frequency of discovery for some cell types. In all scenarios above, an in-silico prediction of the missing population can lead to an informed decision about conducting new experiments or not.

Multiple methods for perturbation response modeling have been developed based on autoencoders (AE)[Amodio et al., 2018, Lotfollahi et al., 2020, Lotfollahi et al., 2021, Lotfollahi et al., 2019, Russkikh et al., 2020, Wei et al., 2022, Yuan et al., 2021], a deep learning architecture to learn a low-dimensional representation of the data.

Variational autoencoders

The fundamental principle of autoencoders is that they are composed of two parts, an encoder and a decoder. The encoder tries to learn a latent space of the input data (usually gene expression) which can be decoded with minimal reconstruction error by the decoder. The latent space is usually of a lower dimension than the input space. An extension of AEs are variational autoencoders (VAE) that address the issue of non-regularized latent spaces of AEs by providing generative capability to the entire space. A non-regularized latent space only really provides strong sampling capability for the distinct classes that formed clusters. The famous MNIST dataset of handwritten digits would only allow the sampling of the digits 0-9 in any of the determined 10 clusters. However, it would result in garbage input if sampling were attempted outside the clusters. Whereas, the encoder in AEs outputs latent vectors, the encoder in VAEs outputs parameters of a pre-defined distribution in the latent space for every input. The latent space gets regularized by the VAE enforcing a normally distributed latent distribution.

Here, we demonstrate the application of scGen [Lotfollahi et al., 2019], a variational autoencoder combined with vector arithmetics. The model learns a latent representation of the data in which it estimates a difference vector between control (untreated) and perturbed (treated) cells. The estimated difference vector is then added to control cells for the cell type or population of interest to predict the gene expression response for each single cell. Here, we apply scGen to predict the response to IFN-β for a population of CD4-T cells that are artificially held out (unseen) during training to simulate one of the aforementioned real-world scenarios. We again leverage a dataset that contains peripheral blood mononuclear cells (PBMCs) from eight patients with Lupus treated with IFN-β or left untreated from [Kang et al., 2018] across seven different cell-types.

As a first step, we import scanpy and scgen to allow us to work with AnnData objects and employ scGen.

import scanpy as sc
import pertpy as pt

19.3.1. Setting up the Kang dataset for scGen

We will again use pertpy to get the Kang dataset.

adata = pt.dt.kang_2018()

scGen works best with log transformed data. Highly variable gene selection can speed up computations due to the reduced feature space.

sc.pp.log1p(adata)
sc.pp.highly_variable_genes(adata)

We rename label to condition and the conditions themselves for improved readability.

adata.obs.rename({"label": "condition"}, axis=1, inplace=True)
adata.obs["condition"].replace({"ctrl": "control", "stim": "stimulated"}, inplace=True)

This dataset contains PBMCs [Kang et al., 2018] across seven different cell-types.

adata.obs.cell_type.value_counts()

cell_type
CD4 T cells          11238
CD14+ Monocytes       5697
B cells               2651
NK cells              1716
CD8 T cells           1621
FCGR3A+ Monocytes     1089
Dendritic cells        529
Megakaryocytes         132
Name: count, dtype: int64

We remove all CD4T cells from the training data (adata_t) to simulate a real-world scenario of not capturing a specific population during an experiment.

adata_t = adata[
    ~(
        (adata.obs["cell_type"] == "CD4 T cells")
        & (adata.obs["condition"] == "stimulated")
    )
].copy()

cd4t_stim = adata[
    (
        (adata.obs["cell_type"] == "CD4 T cells")
        & (adata.obs["condition"] == "stimulated")
    )
].copy()

scGen requires the data to be in a particular format which is facilitated through AnnData and the setup_anndata function. It requires the key of the sample, the batch_key (in our case, "condition") and the cell type label key, the labels_key ("cell_type").

pt.tl.SCGEN.setup_anndata(adata_t, batch_key="condition", labels_key="cell_type")

19.3.2. Model construction and training

scGen requires the modified AnnData object (adata_t) to construct the model object, which can be used to train the model. This function receives multiple user inputs, including the number of nodes in each hidden layer (n_hidden) of the model before the bottleneck layer (the middle layer of the network) and also the number of such layers (n_layers). Additionally, the user can adapt the dimension of the bottleneck layer, which is used to calculate the difference vector between perturbed cells and control cells. The default parameters used here are taken from the original publication. In practice, wider hidden layers lead to better reconstruction accuracy, which is essential for our aim to predict the perturbation response across many genes.

model = pt.tl.SCGEN(adata_t, n_hidden=800, n_latent=100, n_layers=2)

scGen is a neural network with thousands of parameters to learn a low-dimensional data representation. Here, we use train method to estimate these parameters using the training data. There are multiple parameters here, max_epochs is the maximum number of iterations the model is allowed to update its parameters which are set to 100 here. The higher values training epochs will take more computation time but might help better results. The batch_size is the number of samples (individual cells) the model sees to update its parameters. Lower numbers usually lead to better results in the case of scGen. Finally, there is early_stopping, which enables the model to stop the training if its results are not improved after early_stopping_patience training epochs. The early stopping mechanism prevents potential overfitting of the training data, which can lead to poor generalization to unseen populations.

model.train(
    max_epochs=100, batch_size=32, early_stopping=True, early_stopping_patience=25
)

INFO     Jax module moved to TFRT_CPU_0.Note: Pytorch lightning will show GPU is not being used for the Trainer.   

GPU available: False, used: False
TPU available: False, using: 0 TPU cores
IPU available: False, using: 0 IPUs
HPU available: False, using: 0 HPUs

Epoch 26/100:  26%|██▌       | 26/100 [1:28:13<4:11:07, 203.61s/it, v_num=1, train_loss_step=1.06e+3, train_loss_epoch=4.52e+3]
Monitored metric elbo_validation did not improve in the last 25 records. Best score: 479.507. Signaling Trainer to stop.

To visualize the learned representation of data by the model, we plot the latent representation of the model using the UMAP algorithm. The get_latent_representation() returns a 100-dimensional vector for each cell. We store the latent representations in the .obsm slot of the AnnData object.

adata_t.obsm["scgen"] = model.get_latent_representation()

Next, we recalculate the neighbors graph and the UMAP embedding using the calculated latent representation to finally visualize the new embedding in a UMAP plot.

sc.pp.neighbors(adata_t, use_rep="scgen")
sc.tl.umap(adata_t)

sc.pl.umap(adata_t, color=["condition", "cell_type"], wspace=0.4, frameon=False)

As observed above, the IFN-β stimulation induced strong transcriptional changes across all cell-types

19.3.3. Predicting CD4T responses to IFN-β stimulation

After the model is trained, we can ask the model to simulate the effect of IFN-β response for each control CD4T cell present in the training data. The prediction is made possible via the predict method, which receives the corresponding labels (ctrl_key and stim_key below) in the condition (as provided earlier by the user) column of the AnnData object to estimate a global the difference vector in the latent space between ‘control’ and ‘stimulated’ cells. This vector is then added to each single-cell present specified in celltype_to_predict (here CD4T).

pred, delta = model.predict(
    ctrl_key="control", stim_key="stimulated", celltype_to_predict="CD4 T cells"
)

# we annotate the predicted cells to distinguish them later from ground truth cells.
pred.obs["condition"] = "predicted stimulated"

INFO     Received view of anndata, making copy.                                                                    
INFO     Input AnnData not setup with scvi-tools. attempting to transfer AnnData setup                             

INFO     Received view of anndata, making copy.                                                                    
INFO     Input AnnData not setup with scvi-tools. attempting to transfer AnnData setup                             
INFO     Received view of anndata, making copy.                                                                    
INFO     Input AnnData not setup with scvi-tools. attempting to transfer AnnData setup                             

19.3.4. Evaluating the predicted IFN-β response

In previous sections, we predicted the response to IFN-β for each CD4T cell present among the control population. Since single-cell sequencing is destructive, meaning that cells can not be measured before and after a particular perturbation, it is impossible to directly evaluate the prediction for the same cell after IFN-β stimulation. However, we have a group of cells in the data treated with IFN-β, which we can use to measure how well the predicted cell population aligns with ground truth cells. To pursue this, we evaluate predictions qualitatively by looking at the embedding of control, predicted, and actual CD4T IFN-β cells in principal component analysis (PCA) space. Additionally, we also quantitatively measure the correlation between mean gene expression of predicted cells and IFN-β across all genes and differentially expressed genes after IFN-β stimulaton.

First, we construct an AnnData object containing control, predicted stimulated, and actual stimulated cells.

ctrl_adata = adata[
    ((adata.obs["cell_type"] == "CD4 T cells") & (adata.obs["condition"] == "control"))
]
# concatenate pred, control and real CD4 T cells in to one object
eval_adata = ctrl_adata.concatenate(cd4t_stim, pred)

eval_adata.obs.condition.value_counts()

condition
stimulated              5678
control                 5560
predicted stimulated    5560
Name: count, dtype: int64

We first look at the PCA co-embedding of control, IFN-β stimulated and predicted CD4T cells.

sc.tl.pca(eval_adata)
sc.pl.pca(eval_adata, color="condition", frameon=False)

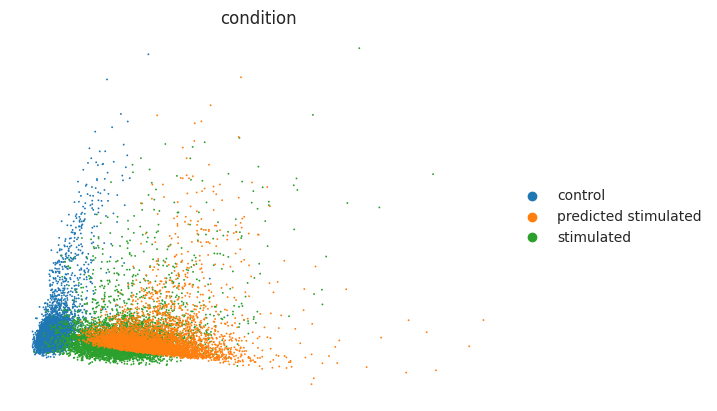
As observed above, the predicted stimulated cells were moved towards the CD4T stimulated cells with IFN-β. Yet we should also look at differentially expressed genes (DEGs) to verify whether the most striking DE genes are also present in the predicted stimulated cells. Below, we look at the overall mean correlation between predicted and real cells. Before that, we extract DEGs between control and stimulated cells:

cd4t_adata = adata[adata.obs["cell_type"] == "CD4 T cells"]

We estimate DEGs using scanpy’s implementation of the Wilcoxon test.

sc.tl.rank_genes_groups(cd4t_adata, groupby="condition", method="wilcoxon")
diff_genes = cd4t_adata.uns["rank_genes_groups"]["names"]["stimulated"]
diff_genes

array(['ISG15', 'IFI6', 'ISG20', ..., 'EEF1A1', 'FTH1', 'RGCC'],
      dtype=object)

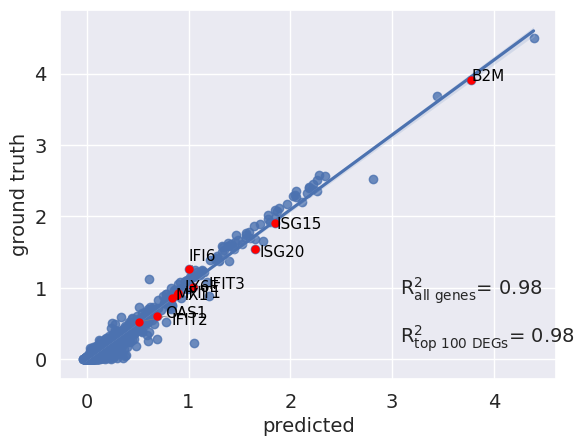
scGen features a reg_mean_plot that calculates the R² correlation between mean gene expression of predicted and existing IFN-β cells. The higher the R² (max is 1), the more faithful is the prediction compared to the ground truths. The highlighted genes in red are the top 10 upregulated DEGs after IFN-β stimulation, which are essential for a successful prediction. As observed, the model did a good job for genes with higher mean values, while it failed for some genes with a mean expression between 0-1. We also measure accuracy across non-DEGs because the model should not change genes not affected by the perturbation while changing the expression of DEGs.

from scvi import REGISTRY_KEYS

r2_value = model.plot_reg_mean_plot(
    eval_adata,
    condition_key="condition",
    axis_keys={"x": "predicted stimulated", "y": "stimulated"},
    gene_list=diff_genes[:10],
    top_100_genes=diff_genes,
    labels={"x": "predicted", "y": "ground truth"},
    show=True,
    legend=False,
)

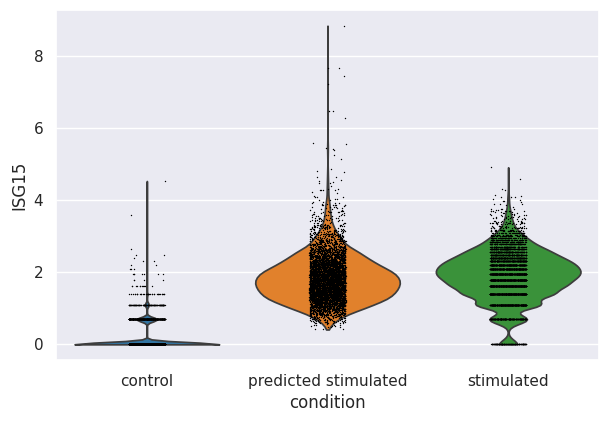
We can additionally look at the distribution of the top upregulated genes by IFN-β. For example, we plotted the distribution of expression in ISG15, a well-known gene induced after IFN stimulation. As observed, the model identified that this gene should be upregulated after stimulation with IFN-β, and it indeed shifted values to a similar range in ground-truth (stimulated) cells.

sc.pl.violin(eval_adata, keys="ISG15", groupby="condition")

Overall, we demonstrated the application of scGen as an example of perturbation response models in predicting gene expression of the unseen population under desired perturbations. While perturbation response models provide in silico predictions, they cannot replace performing actual experiments. It is also unclear how much of the predicted response is attributed to cell type specific responses or across cell types. However, as observed in the case of scGen, it can predict the overall response for highly expressed genes yet provide poorer predictions for lowly expressed genes, which requires further optimization and motivation for developing more sophisticated and robust approaches.

19.4. Analysing single-pooled CRISPR screens

Expanded CRISPR-compatible CITE-seq (ECCITE-seq) enables the capture of single guide RNA (sgRNA) sequences together with transcriptome and surface protein measurements in the form of antibody-derived tags (ADTs). This allows for the application of many genetic perturbations together with transcriptomics readouts for effect exploration and validation of the perturbations through protein expression, making this assay very powerful. However, this power comes not only with great responsibility, but also with complexity.

Fig. 19.1 ECCITE-seq overview. mRNA is measured together with surface protein expression using antibody derived tags. Biological replicates are resolved through hashtag-derived oligonucleotides. The assignment of the guide RNAs is done using guide-derived oligonucleotides. Image obtained from (https://cite-seq.com/eccite-seq).

For the purpose of this analysis we will be using the Papalexi 2021 dataset [Papalexi et al., 2021]. This dataset contains about 20000 stimulated THP-1 cells that used 111 gRNAs. THP-1 cells stimulated with a combination of IFN-y, decitabine (DAC) and transforming growth factor (TGF)-β1 results in an induction of three immune checkpoints: programmed death-ligand 1 (PD-L1), PD-L2 and CD86. The goal of the ECCITE-seq experiment was to investigate molecular networks that regulate PD-L1 expression, because it is frequently observed in human cancers and can suppress T-cell-mediated immune responses [Papalexi et al., 2021].

For this specific analysis, we want to:

1. Remove confounding sources of variation such as cell cycle effects or batch effects.

2. Determine which cells were affected by the desired perturbations and which cells escaped.

3. Visualize perturbation responses.

To conduct this analysis we will again use pertpy which implements the Mixscape pipeline for the scverse ecosystem about 5-10x faster. This pipeline was originally developed for the Seurat ecosystem, and we largely follow the accompanying Seurat Vignette (https://satijalab.org/seurat/articles/mixscape_vignette.html).

We start by importing pertpy, scanpy and muon, which we will require for the preprocessing of the protein data.

import pertpy as pt
import muon as mu
import scanpy as sc

As a first step we fetch the dataset using pertpy. The return type of the dataloader is a MuData object containing the transcriptomics measurements, the ADT measurements and guide RNA counts.

mdata = pt.dt.papalexi_2021()
mdata

MuData object with n_obs × n_vars = 20729 × 18776
  4 modalities
    rna:	20729 x 18649
      obs:	'orig.ident', 'nCount_RNA', 'nFeature_RNA', 'nCount_HTO', 'nFeature_HTO', 'nCount_GDO', 'nCount_ADT', 'nFeature_ADT', 'percent.mito', 'MULTI_ID', 'HTO_classification', 'guide_ID', 'gene_target', 'NT', 'perturbation', 'replicate', 'S.Score', 'G2M.Score', 'Phase'
      var:	'name'
    adt:	20729 x 4
      obs:	'orig.ident', 'nCount_RNA', 'nFeature_RNA', 'nCount_HTO', 'nFeature_HTO', 'nCount_GDO', 'nCount_ADT', 'nFeature_ADT', 'percent.mito', 'MULTI_ID', 'HTO_classification', 'guide_ID', 'gene_target', 'NT', 'perturbation', 'replicate', 'S.Score', 'G2M.Score', 'Phase'
      var:	'name'
    hto:	20729 x 12
      obs:	'orig.ident', 'nCount_RNA', 'nFeature_RNA', 'nCount_HTO', 'nFeature_HTO', 'nCount_GDO', 'nCount_ADT', 'nFeature_ADT', 'percent.mito', 'MULTI_ID', 'HTO_classification', 'guide_ID', 'gene_target', 'NT', 'perturbation', 'replicate', 'S.Score', 'G2M.Score', 'Phase'
      var:	'name'
    gdo:	20729 x 111
      obs:	'orig.ident', 'nCount_RNA', 'nFeature_RNA', 'nCount_HTO', 'nFeature_HTO', 'nCount_GDO', 'nCount_ADT', 'nFeature_ADT', 'percent.mito', 'MULTI_ID', 'HTO_classification', 'guide_ID', 'gene_target', 'NT', 'perturbation', 'replicate', 'S.Score', 'G2M.Score', 'Phase'
      var:	'name'

The original Seurat object contained four assays which were transformed into individual AnnData objects to then create the here downloaded MuData object. The individual modalities are:

1. adt: A count matrix of the four captured antibody-derived tags (CD86, PDL1, PDL2, CD366) which are also commonly simply referred to as “proteins” in this setting.

2. gdo: The 111 used guide RNAs (gRNA). To assign a gRNA identity to each cell, guide-derived oligonucleotide (GDO) counts were examined. If a cell had less than five counts for all gRNA sequences, it was classified as negative. For all other cells, the gRNA with the highest number of counts was assigned to that cell. Cells that had high counts for more than one gRNA were classified as doublets.

3. hto: To keep track of the identity of each biological replicate, the samples were hashed using hashtag-derived oligonucleotides (HTO) following the cell hashing protocol [Stoeckius et al., 2018].

4. rna: This corresponds to the transcriptome measurements for all cells and is the usual cells by genes count matrix.

19.4.1. Preprocessing

We keep the preprocessing of the RNA and ADTs simple. First, we normalize the RNA using scanpy’s normalize_total followed by log transformation and highly variable gene selection. To normalize the ADTs we apply centered log ration transformation [Stoeckius et al., 2017].

sc.pp.normalize_total(mdata["rna"])
sc.pp.log1p(mdata["rna"])
sc.pp.highly_variable_genes(mdata["rna"], subset=True)

mu.prot.pp.clr(mdata["adt"])

19.4.2. Data exploration

To get a feeling for our dataset we visualize the replicates, cell-cycle phases and perturbations in a UMAP embedding.

sc.pp.pca(mdata["rna"])

# We calculate neighbors with the cosine distance similarly to the original Seurat implementation
sc.pp.neighbors(mdata["rna"], metric="cosine")

sc.tl.umap(mdata["rna"])

sc.pl.umap(mdata["rna"], color=["replicate", "Phase", "perturbation"])

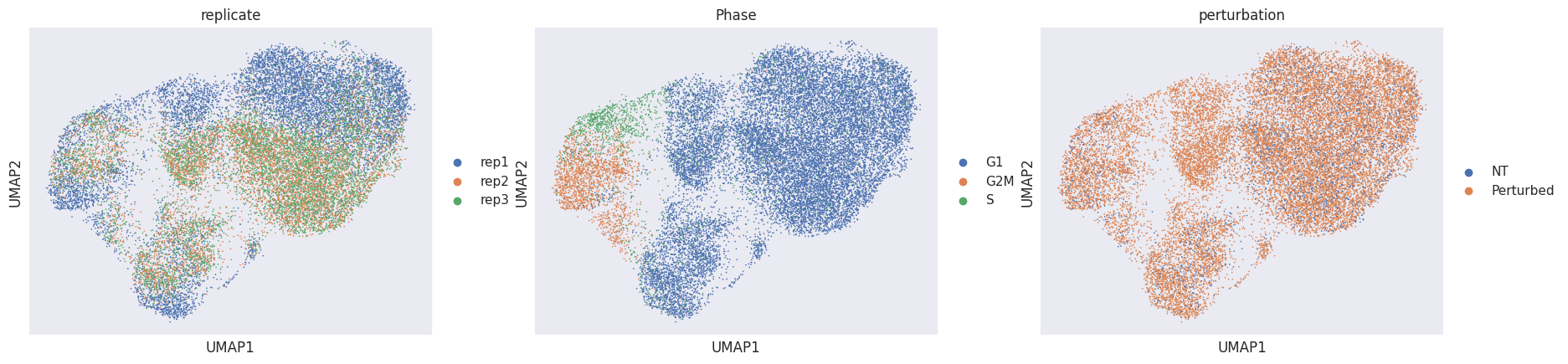
When glancing at the UMAPs we identify two clearly visible issues:

1. Many cells are separated by replicate ID. This is a common sign of a batch effect.

2. The cell cycle phase is a confounder in the embedding.

Hence, we now try to project our cells into a perturbation space by calculating local perturbation signatures to mitigate these identified issues.

19.4.3. Calculating local perturbation signatures

To alleviate the aforementioned issues, we will calculate local perturbation signatures. The core idea is that by subtracting the averaged expression of the k nearest cells from the control pool (=NT) from every cell, we retrieve the component of every cell that solely reflects the genetic perturbation. The k nearest neighbors must be in a biological state matching the target cell, but are not allowed to have been targeted by any gRNA. The obtained component is denoted as the local perturbation signature. By default, the number of neighbors k is set to 20. Following the recommendations of Papalexi et al., we recommend setting from the range of 20 < k 30. A k that is too small or too large is unlikely to remove any technical variation from the dataset [Papalexi et al., 2021].

We now create a Mixscape object using pertpy and calculate the perturbation signature.

ms = pt.tl.Mixscape()

ms.perturbation_signature(
    mdata["rna"],
    pert_key="perturbation",
    control="NT",
    split_by="replicate",
    n_neighbors=20,
)

# We create a copy of the object to recalculate the PCA.
# Alternatively we could replace the X of the RNA part of our MuData object with the `X_pert` layer.
adata_pert = mdata["rna"].copy()
adata_pert.X = adata_pert.layers["X_pert"]
sc.pp.pca(adata_pert)
sc.pp.neighbors(adata_pert, metric="cosine")
sc.tl.umap(adata_pert)
sc.pl.umap(adata_pert, color=["replicate", "Phase", "perturbation"])

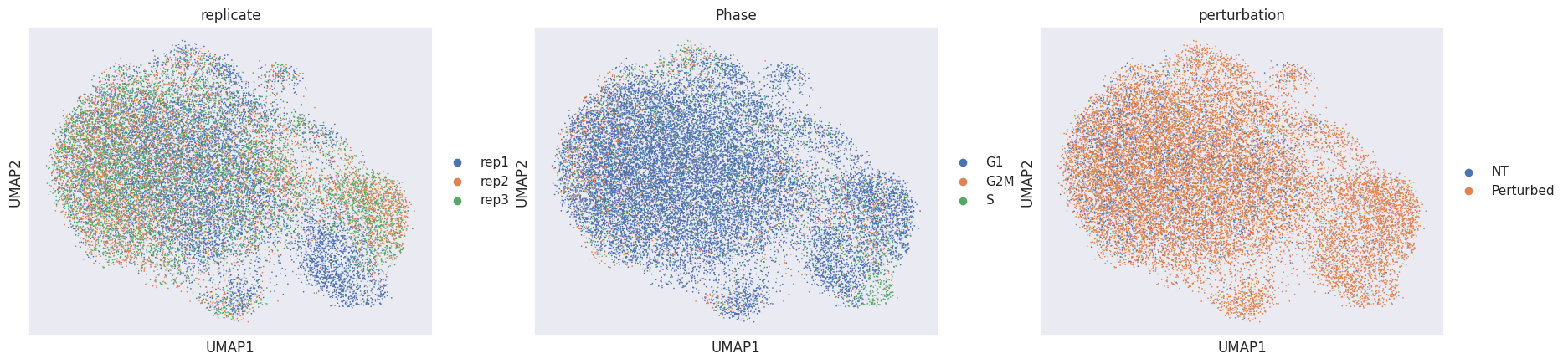
Using the perturbation signature to calculate the neighbors graph and the eventual embedding removes technical variation and reveals one additional perturbation-specific cluster. Now that our data is mostly free of confounding effects, we need to determine for which targeted cells (=perturbed) the perturbation was successful (=KO) or not (=NP).

19.4.4. Identifying cells with no detectable perturbation

The primary assumption that we make is that every target gene class is a mixture of two Gaussian distributions. One of these represents the successful knockouts (KO) and the other the non-perturbed (NP) cells. The distribution of the NP cells should then be identical to the cells expressing non-targeting gRNAs (NT). After having estimated the distribution of the KO cells, Mixscape calculates the posterior probability that a cell belongs to the KO distribution and classifies cells with a probability of more than 0.5 as KOs. Applying this to all 11 target gene classes allows us to identify all KO cells while evaluating the targeting efficacy of the different gRNAs.

ms.mixscape(adata=mdata["rna"], control="NT", labels="gene_target", layer="X_pert")

We can now plot the class distributions for all 111 gRNAs.

ms.plot_barplot(mdata["rna"], guide_rna_column="guide_ID")

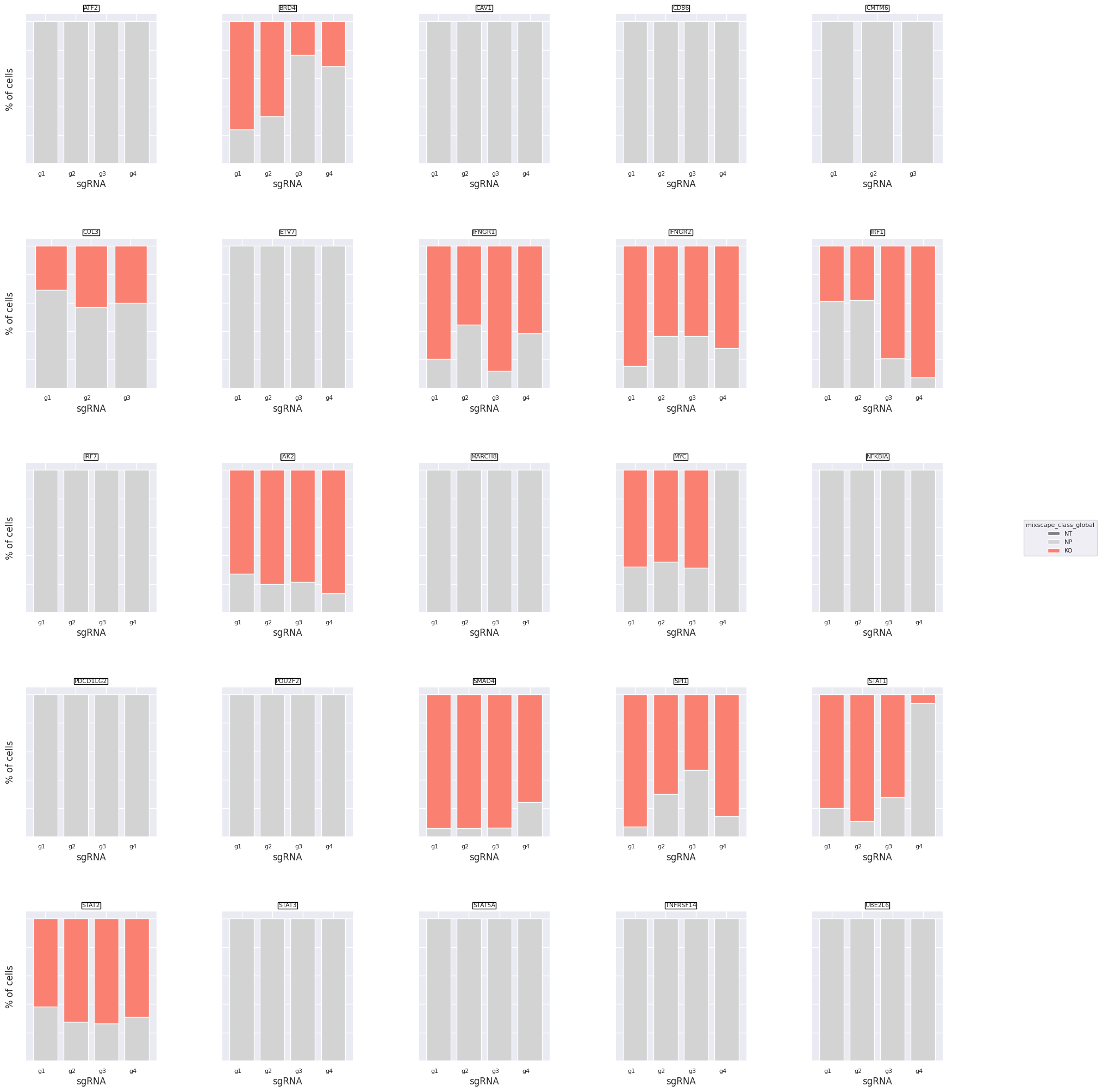
<Axes: title={'center': 'UBE2L6'}, xlabel='sgRNA', ylabel='% of cells'>

We detect variation in gRNA targeting efficiency within each class. For example gRNA 4 for STAT1 did not seem to be very effective, but gRNA 1-3 were.

Let’s inspect the perturbation scores of an example target gene (IFNGR2).

ms.plot_perturbscore(
    adata=mdata["rna"], labels="gene_target", target_gene="IFNGR2", color="orange"
)

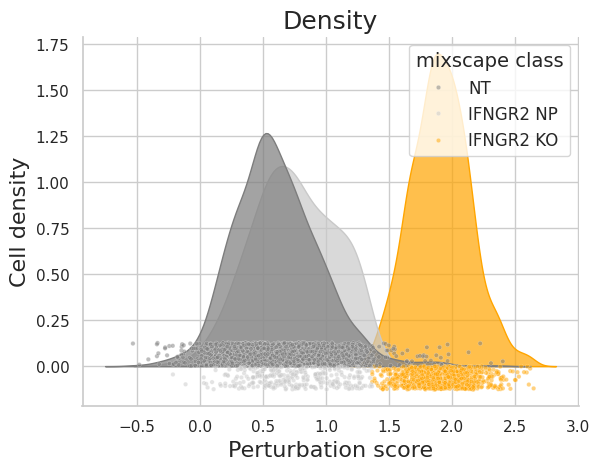
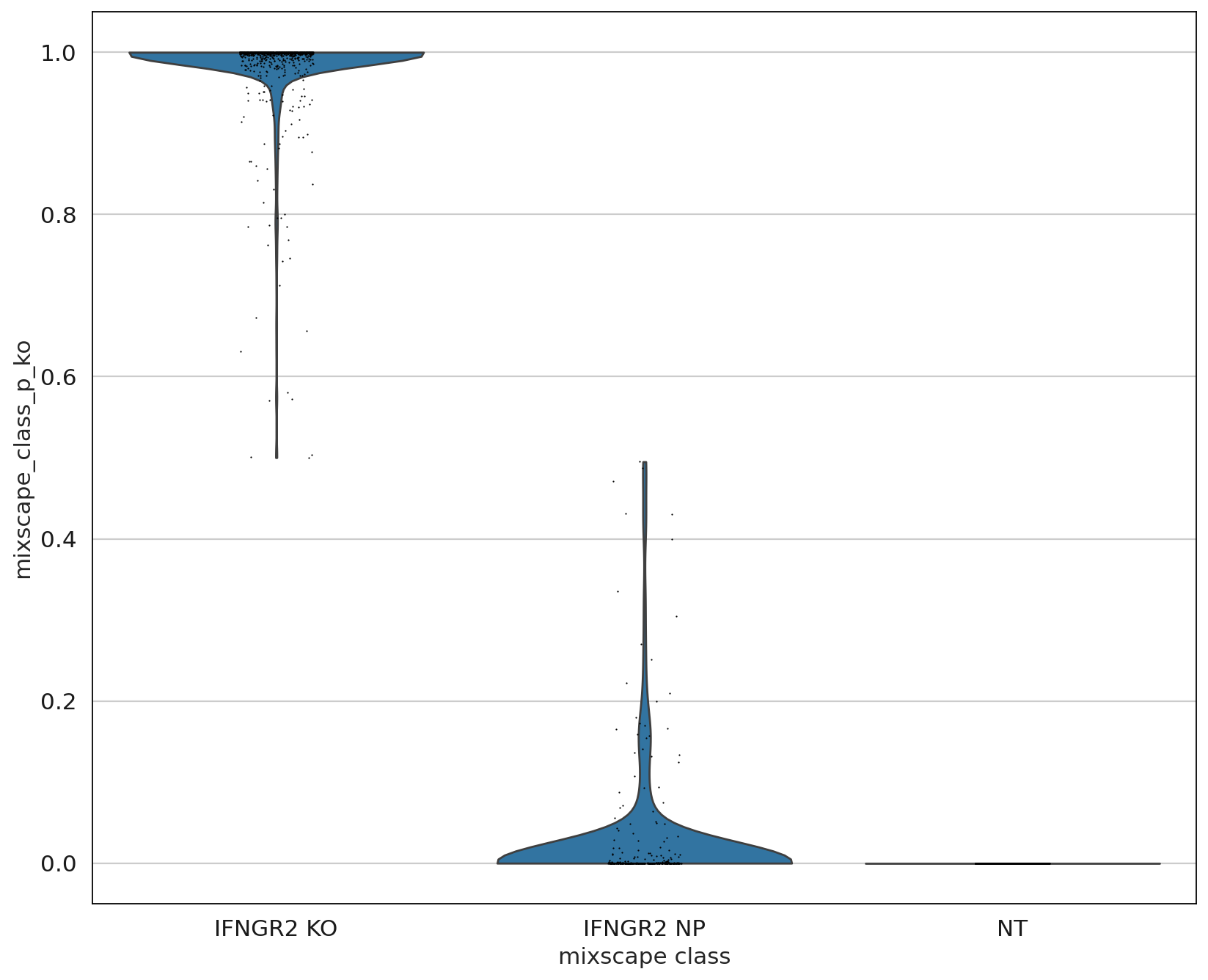
As expected, the distributions of the NT and IFNGR2 NP classes match rather well, whereas the IFGNR2 KO distribution is clearly shifted. This should also be reflected in the posterior probabilities.

sc.settings.set_figure_params(figsize=(10, 10))
ms.plot_violin(
    adata=mdata["rna"],
    target_gene_idents=["NT", "IFNGR2 NP", "IFNGR2 KO"],
    groupby="mixscape_class",
)

The posterior probabilities clearly separate the two classes highlighting very few unclear cases. This can be further highlighted by running a simple DE test between the mixscape classes and visualizing the results on a heatmap by ordering the posterior probabilities.

ms.plot_heatmap(
    adata=mdata["rna"],
    labels="gene_target",
    target_gene="IFNGR2",
    layer="X_pert",
    control="NT",
)

WARNING: dendrogram data not found (using key=dendrogram_mixscape_class). Running `sc.tl.dendrogram` with default parameters. For fine tuning it is recommended to run `sc.tl.dendrogram` independently.
WARNING: Groups are not reordered because the `groupby` categories and the `var_group_labels` are different.
categories: IFNGR2 KO, IFNGR2 NP, NT
var_group_labels: NT

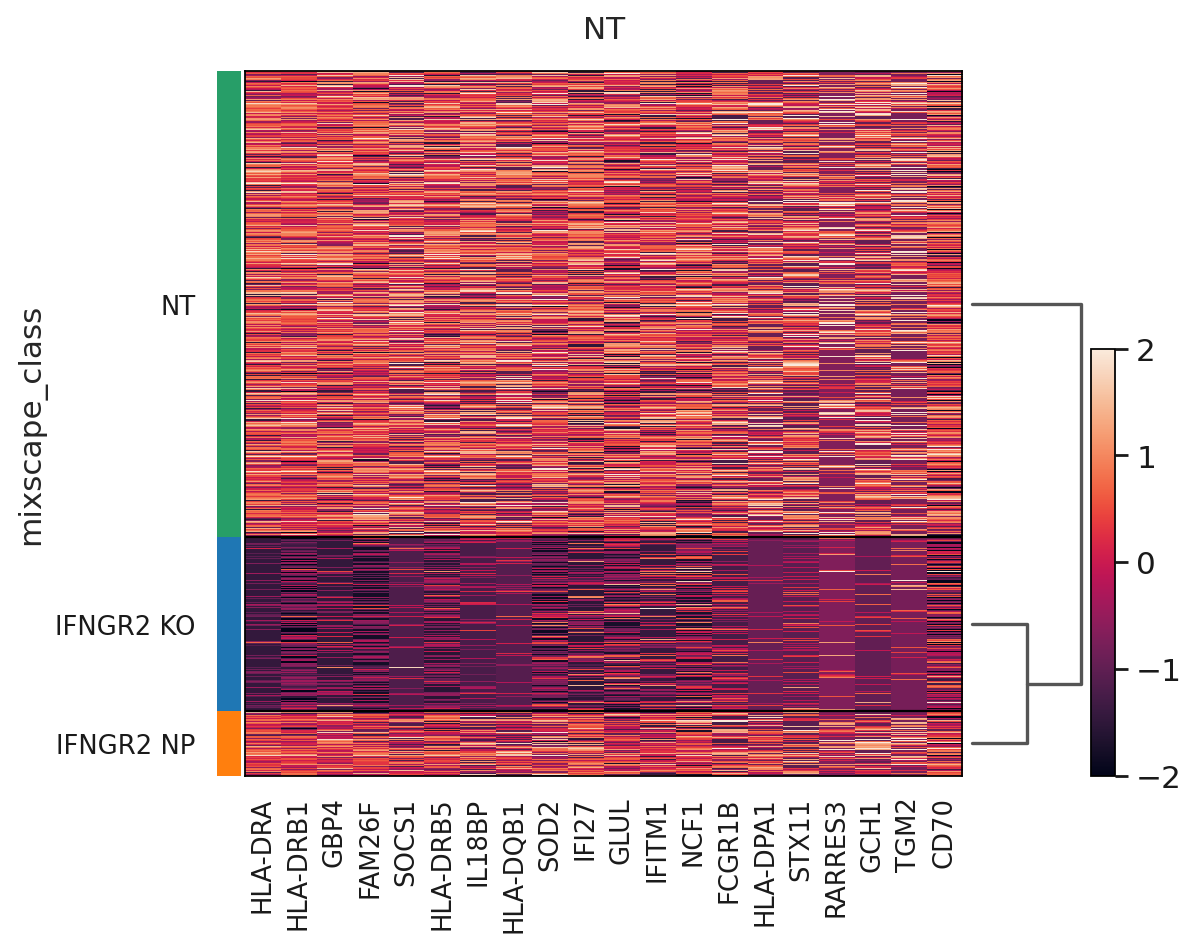
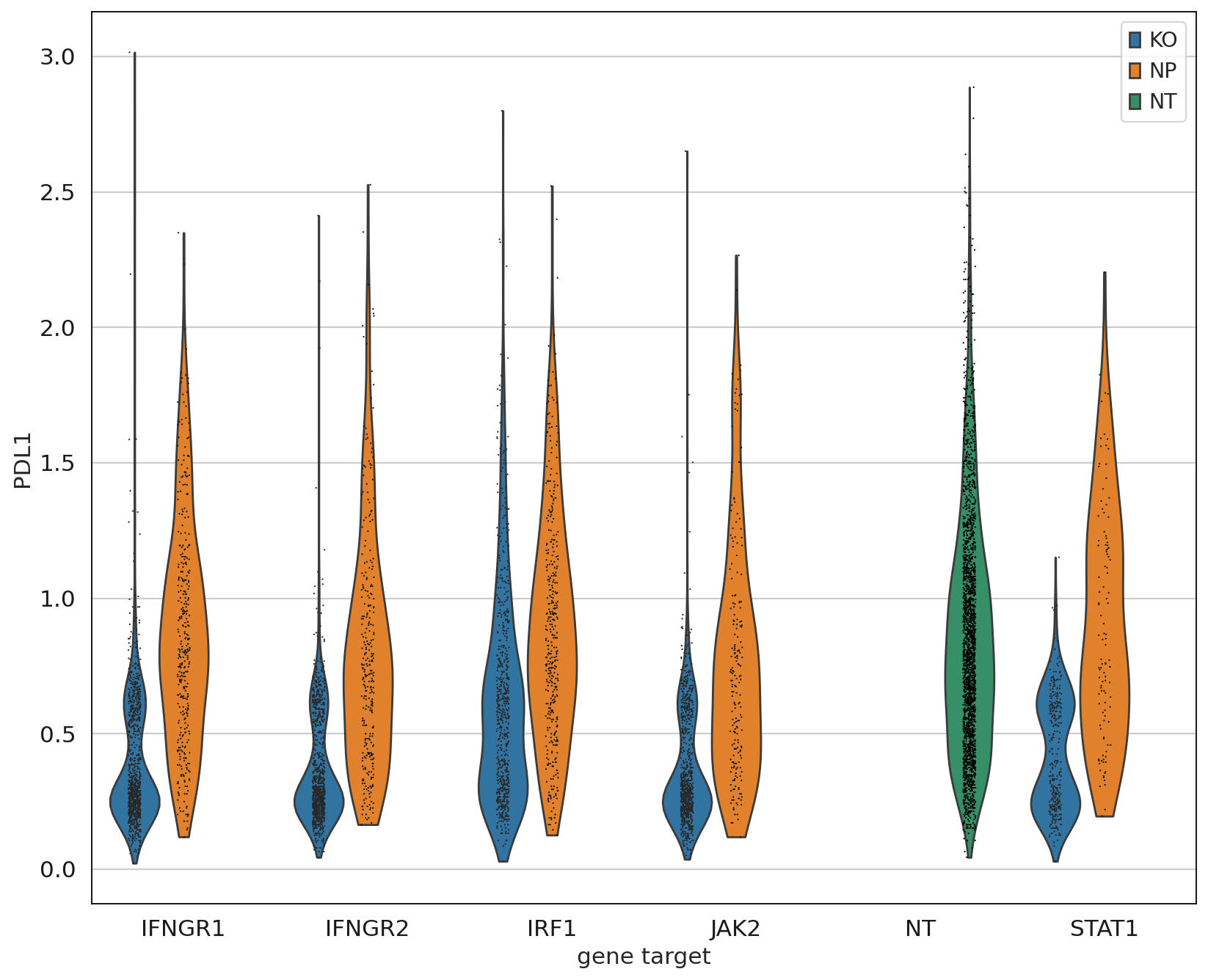
Up to this point we have only been working with the transcriptomics data, but we can now leverage the measured proteins to demonstrate that only IFGN pathway KO cells have a reduction in PDL1 expression.

mdata["adt"].obs["mixscape_class_global"] = mdata["rna"].obs["mixscape_class_global"]
ms.plot_violin(
    adata=mdata["adt"],
    target_gene_idents=["NT", "JAK2", "STAT1", "IFNGR1", "IFNGR2", "IRF1"],
    keys="PDL1",
    groupby="gene_target",
    hue="mixscape_class_global",
)

19.4.5. Visualizing perturbation responses with Linear Discriminant Analysis

The final step in the Mixscape pipeline is to calculate and visualize perturbation-specific clusters. This is done by applying linear discriminant analysis (LDA) and recalculating the UMAP using the determined results. LDA attempts to maximize the separability of known labels, which are the mixscape classes in our case, using both gene expression and the labels.

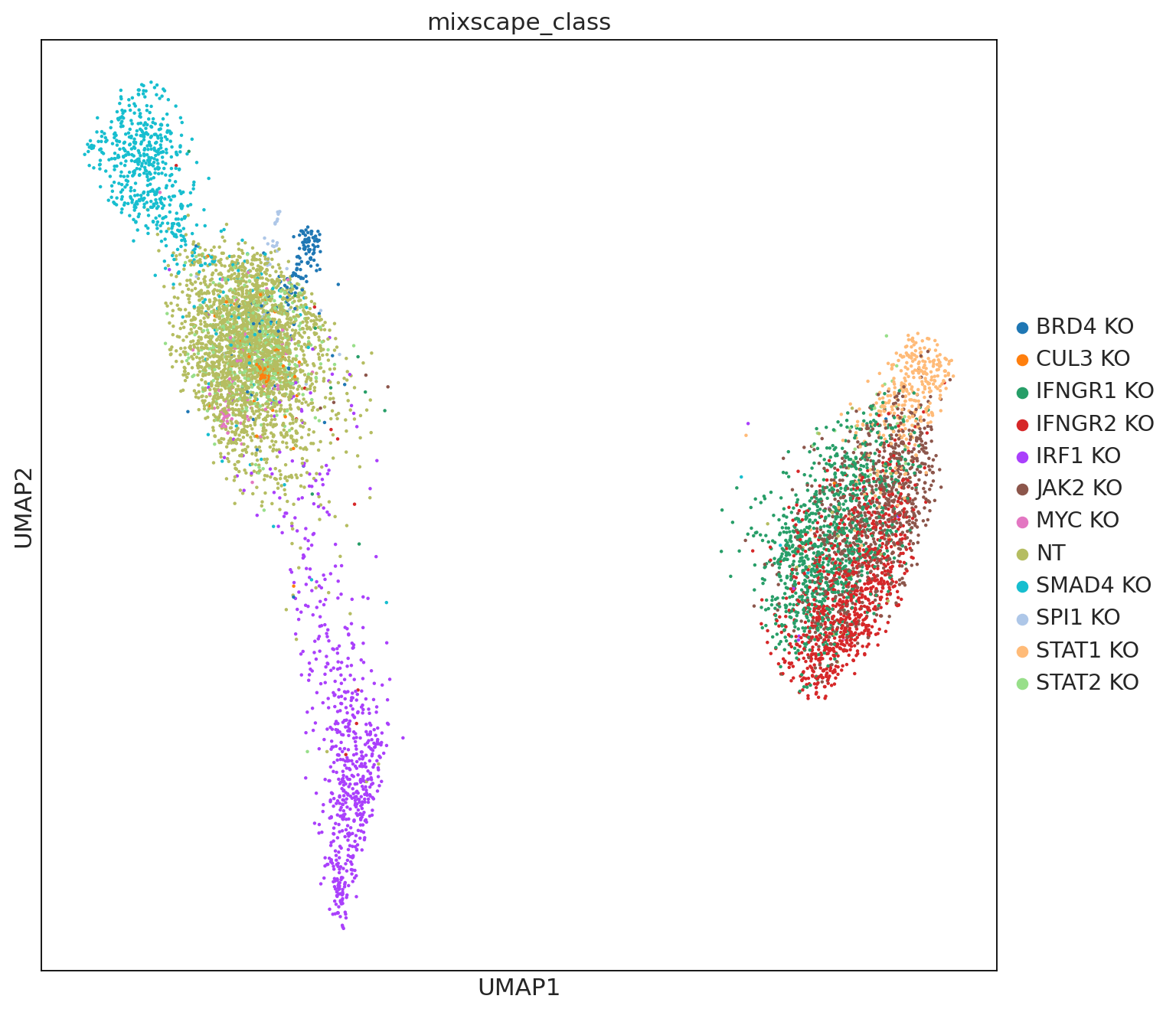
ms.lda(adata=mdata["rna"], control="NT", labels="gene_target", layer="X_pert")

ms.plot_lda(adata=mdata["rna"], control="NT")

The LDA highlights at least two major types of perturbations as evident by the two islands. However, we want to emphasize that only more stringent analyses, such as pathway analysis followed by biological validation, could determine that several knockouts have similar effects.

19.5. Key Takeaways

1. When applying Augur ensure that the cell types can be confidently labeled. Use differential abundance tests to find confounding effects and differential gene expression to find gene-level sources of perturbation effects.

2. Predicting perturbation responses with tools such as scGen works well for highly expressed genes, but is challenging for lowly expressed genes.

3. The linear discriminant analysis step of the Mixscape pipeline primarily aids with visualization. Distances in UMAPs should be interpreted with caution and therefore similarities and differences between knockouts cannot always be inferred at a glance.

19.6. Quiz

1. Why is it required to have confident cell type labels when applying Augur?

2. Why should scGen primarily only be applied to highly expressed genes?

3. The mixscape pipeline results in clusters of genetic perturbations. Why must the distances in the UMAPs be interpreted with caution? What does it mean when some genetic perturbations are close or distant in the UMAP embedding?

19.7. References

[pemoAvDM+18]

Matthew Amodio, David van Dijk, Ruth Montgomery, Guy Wolf, and Smita Krishnaswamy. Out-of-sample extrapolation with neuron editing. arXiv preprint arXiv:1805.12198, 2018.

[pemoBDC+19]

Aritra Bhattacherjee, Mohamed Nadhir Djekidel, Renchao Chen, Wenqiang Chen, Luis M. Tuesta, and Yi Zhang. Cell type-specific transcriptional programs in mouse prefrontal cortex during adolescence and addiction. Nature Communications, 10(1):4169, Sep 2019. URL: https://doi.org/10.1038/s41467-019-12054-3, doi:10.1038/s41467-019-12054-3.

[pemoFMT+21]

Chris J Frangieh, Johannes C Melms, Pratiksha I Thakore, Kathryn R Geiger-Schuller, Patricia Ho, Adrienne M Luoma, Brian Cleary, Livnat Jerby-Arnon, Shruti Malu, Michael S Cuoco, and others. Multimodal pooled perturb-cite-seq screens in patient models define mechanisms of cancer immune evasion. Nature genetics, 53(3):332–341, 2021.

[pemoJLWT21] (1,2)

Yuge Ji, Mohammad Lotfollahi, F Alexander Wolf, and Fabian J Theis. Machine learning for perturbational single-cell omics. Cell Systems, 12(6):522–537, 2021.

[pemoKST+18] (1,2,3,4,5,6,7)

Hyun Min Kang, Meena Subramaniam, Sasha Targ, Michelle Nguyen, Lenka Maliskova, Elizabeth McCarthy, Eunice Wan, Simon Wong, Lauren Byrnes, Cristina M Lanata, and others. Multiplexed droplet single-cell term`rna`-sequencing using natural genetic variation. Nature biotechnology, 36(1):89–94, 2018.

[pemoLNTW20]

Mohammad Lotfollahi, Mohsen Naghipourfar, Fabian J Theis, and F Alexander Wolf. Conditional out-of-distribution generation for unpaired data using transfer vae. Bioinformatics, 36(Supplement_2):i610–i617, 2020.

[pemoLSDD+21]

Mohammad Lotfollahi, Anna Klimovskaia Susmelj, Carlo De Donno, Yuge Ji, Ignacio L Ibarra, F Alexander Wolf, Nafissa Yakubova, Fabian J Theis, and David Lopez-Paz. Learning interpretable cellular responses to complex perturbations in high-throughput screens. bioRxiv, 2021.

[pemoLWT19] (1,2)

Mohammad Lotfollahi, F Alexander Wolf, and Fabian J Theis. Scgen predicts single-cell perturbation responses. Nature methods, 16(8):715–721, 2019.

[pemoPMB+21] (1,2,3,4,5)

Efthymia Papalexi, Eleni P. Mimitou, Andrew W. Butler, Samantha Foster, Bernadette Bracken, William M. Mauck, Hans-Hermann Wessels, Yuhan Hao, Bertrand Z. Yeung, Peter Smibert, and Rahul Satija. Characterizing the molecular regulation of inhibitory immune checkpoints with multimodal single-cell screens. Nature Genetics, 53(3):322–331, Mar 2021. URL: https://doi.org/10.1038/s41588-021-00778-2, doi:10.1038/s41588-021-00778-2.

[pemoRSP+21]

Joseph M Replogle, Reuben A Saunders, Angela N Pogson, Jeffrey A Hussmann, Alexander Lenail, Alina Guna, Lauren Mascibroda, Eric J Wagner, Karen Adelman, Jessica L Bonnar, and others. Mapping information-rich genotype-phenotype landscapes with genome-scale perturb-seq. bioRxiv, 2021.

[pemoRAS+20]

Nikolai Russkikh, Denis Antonets, Dmitry Shtokalo, Alexander Makarov, Yuri Vyatkin, Alexey Zakharov, and Evgeny Terentyev. Style transfer with variational autoencoders is a promising approach to term`rna`-seq data harmonization and analysis. Bioinformatics, 36(20):5076–5085, 2020.

[pemoSSK+21]

Michael A. Skinnider, Jordan W. Squair, Claudia Kathe, Mark A. Anderson, Matthieu Gautier, Kaya J. E. Matson, Marco Milano, Thomas H. Hutson, Quentin Barraud, Aaron A. Phillips, Leonard J. Foster, Gioele La Manno, Ariel J. Levine, and Grégoire Courtine. Cell type prioritization in single-cell data. Nature Biotechnology, 39(1):30–34, Jan 2021. URL: https://doi.org/10.1038/s41587-020-0605-1, doi:10.1038/s41587-020-0605-1.

[pemoSGK+21]

Jordan W. Squair, Matthieu Gautier, Claudia Kathe, Mark A. Anderson, Nicholas D. James, Thomas H. Hutson, Rémi Hudelle, Taha Qaiser, Kaya J. E. Matson, Quentin Barraud, Ariel J. Levine, Gioele La Manno, Michael A. Skinnider, and Grégoire Courtine. Confronting false discoveries in single-cell differential expression. Nature Communications, 12(1):5692, Sep 2021. URL: https://doi.org/10.1038/s41467-021-25960-2, doi:10.1038/s41467-021-25960-2.

[pemoSSG+21] (1,2,3,4,5,6)

Jordan W. Squair, Michael A. Skinnider, Matthieu Gautier, Leonard J. Foster, and Grégoire Courtine. Prioritization of cell types responsive to biological perturbations in single-cell data with augur. Nature Protocols, 16(8):3836–3873, Aug 2021. URL: https://doi.org/10.1038/s41596-021-00561-x, doi:10.1038/s41596-021-00561-x.

[pemoSMFR+20]

Sanjay R Srivatsan, José L McFaline-Figueroa, Vijay Ramani, Lauren Saunders, Junyue Cao, Jonathan Packer, Hannah A Pliner, Dana L Jackson, Riza M Daza, Lena Christiansen, and others. Massively multiplex chemical transcriptomics at single-cell resolution. Science, 367(6473):45–51, 2020.

[pemoSHS+17]

Marlon Stoeckius, Christoph Hafemeister, William Stephenson, Brian Houck-Loomis, Pratip K. Chattopadhyay, Harold Swerdlow, Rahul Satija, and Peter Smibert. Simultaneous epitope and transcriptome measurement in single cells. Nature Methods, 14(9):865–868, Sep 2017. URL: https://doi.org/10.1038/nmeth.4380, doi:10.1038/nmeth.4380.

[pemoSZHL+18]

Marlon Stoeckius, Shiwei Zheng, Brian Houck-Loomis, Stephanie Hao, Bertrand Z. Yeung, William M. Mauck, Peter Smibert, and Rahul Satija. Cell hashing with barcoded antibodies enables multiplexing and doublet detection for single cell genomics. Genome Biology, 19(1):224, Dec 2018. URL: https://doi.org/10.1186/s13059-018-1603-1, doi:10.1186/s13059-018-1603-1.

[pemoWDW22]

Xiajie Wei, Jiayi Dong, and Fei Wang. Scpregan, a deep generative model for predicting the response of single cell expression to perturbation. Bioinformatics, 2022.

[pemoWMendezMP+22]

Hans-Hermann Wessels, Alejandro Méndez-Mancilla, Efthymia Papalexi, William M Mauck, Lu Lu, John A Morris, Eleni Mimitou, Peter Smibert, Neville E Sanjana, and Rahul Satija. Efficient combinatorial targeting of term`rna` transcripts in single cells with cas13 rna perturb-seq. bioRxiv, 2022.

[pemoYSL+21]

Bo Yuan, Ciyue Shen, Augustin Luna, Anil Korkut, Debora S Marks, John Ingraham, and Chris Sander. Cellbox: interpretable machine learning for perturbation biology with application to the design of cancer combination therapy. Cell systems, 12(2):128–140, 2021.

19.8. Contributors

We gratefully acknowledge the contributions of:

19.8.1. Authors

• Lukas Heumos

• Mohammad Lotfollahi

19.8.2. Reviewers

• Yuge Ji